3)ミカエリス・メンテン式の誘導

　まずは、ミカエリス・メンテン式がどのような式であったかを再度確認していきましょう。

1.ミカエリスメンテン式

　ミカエリス・メンテン式とは、酵素の反応速度vを速度論的な挙動として表したもので、以下の式で表されます。

$$v=\frac{V_{max}[S]}{K_m＋[S]}$$

　・[S]：基質濃度
　・V_max：最大反応速度（基質濃度が無限大の時の反応速度）
　・K_m：v＝Vmax/２（最大反応速度の半分の速度）のときの基質濃度[S]

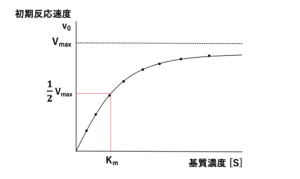
　上図は、酵素濃度[E]が一定の条件下で、さまざまな基質濃度[S]における酵素の初期反応速度v₀を求めて、プロットしたグラフになります。

　このように、基質濃度[S]を変化させると、酵素反応速度も変化することから、さまざまな基質濃度[S]における初期反応速度v₀を求めることにより、ミカエリス・メンテン式で表される曲線を得ることができます。

　それでは、大前提であるミカエリス・メンテン式はどのようにして導き出すことができるのかを見ていきましょう。

2.ミカエリス・メンテン式の導出

　酵素反応では、酵素（E）に基質（S）が結合し、一旦、酵素-基質複合体（ES）を形成した後、生成物（P）が酵素から解離します。

　一般的に、酵素反応式は以下のような式で表されます。

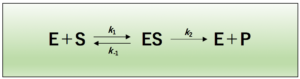
　酵素反応速度の考え方は、反応の最初の段階には生成物 （P）は存在しないということを前提としています。つまり、初期反応では、k₂の逆反応は無視できます。

　この反応は基質の濃度が酵素に比べて十分高ければ全ての酵素がESの形になっていますので、生成物（P）の生成速度は２つ目の反応によって決まり、これが律速段階となります。

　上式から、酵素の反応速度vは、

$$v=-\frac{d[S]}{dt}=\frac{d[P]}{dt}=k_2[ES]\tag{1}$$

と表せます。

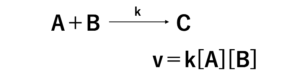
○ミカエリス・メンテン式の前提

　ミカエリス・メンテン式では、前提として上の２つの条件を仮定します（これを「定常状態近似」といいます）。

この仮定のもとでは、[ES]の変化量が0であることから

\begin{eqnarray}\frac{d[ES]}{dt} &=&生成過程-消失過程\\&=& k_1[E][S]-(k_{-1}[ES]＋k_2[ES])=0\end{eqnarray}

と表すことができます。これを整理すると、

$$\frac{d[ES]}{dt}=k_1[E][S]-k_{-1}[ES]-k_2[ES]=0$$

$$(k_2＋k_{-1})[ES]=k_1[E][S]$$

$$[ES]=\frac{k_1}{k_2＋k_{-1}}\times[E][S]$$

$$[ES]=\frac{[E][S]}{K_m}\tag{2}$$

※この$$K_m=\frac{k_{-1}＋k_2}{k_1}$$は、ミカエリス定数と呼ばれます。ミカエリス定数は、ES複合体の生成と分解の速度定数の比と考えることができます。

　ここで、酵素反応における遊離の酵素[E]は、初期の酵素濃度[E]₀からES複合体となった[ES]を引いた値であるので、

$$[E]=[E]_0-[ES]\tag{3} $$

(3)式を(2)式に代入すると

$$[ES]=\frac{([E]_0-[ES])[S]}{K_m}$$

これを整理して、

$$[ES]=\frac{[E]_0[S]-[ES][S]}{K_m}$$

$$K_m[ES]=[E]_0[S]-[ES][S]$$

$$K_m[ES]＋[ES][S]=[E]_0[S]$$

$$(K_m＋[S])[ES]=[E]_0[S]$$

$$[ES]=\frac{[E]_0[S]}{K_m＋[S]}\tag{4} $$

ここで(4)式に(1)式 $$v=k_2[ES]$$を代入すると、

$$v=\frac{k_2[E]_0[S]}{K_m＋[S]}$$

$$v=\frac{V_{max}[S]}{K_m＋[S]}$$

となり、ミカエリス・メンテン式が得られます。

※基質の濃度が酵素に比べて十分高ければすべての酵素がES複合体の形になっていますので、$$V_{max}＝k_2[E]_0$$と表せます。

ミカエリス・メンテン式の誘導についてはこれで以上です。
次は「1)カラムクロマトグラフィーの原理と概要」について学んでいきましょう。

【参考】

Essential細胞生物学(原書第4版)

created by Rinker

• Amazon
• 楽天市場

イラストレイテッド生化学 原書7版 (リッピンコットシリーズ)

created by Rinker

• Amazon
• 楽天市場